一、球形齿轮的基础原理
传统齿轮传动机制回顾
传统齿轮传动系统的核心基础是渐开线齿廓理论。渐开线是当一条直线在圆周上作纯滚动时,直线上任意一点的轨迹所形成的曲线。在齿轮设计中,基圆半径为rb的渐开线方程可表示为:
x = rb(cosφ + φsinφ)
y = rb(sinφ - φcosφ)
其中φ为渐开线的展角参数。这一几何特性确保了齿轮副在啮合过程中保持恒定的传动比,同时具备良好的传动平稳性。
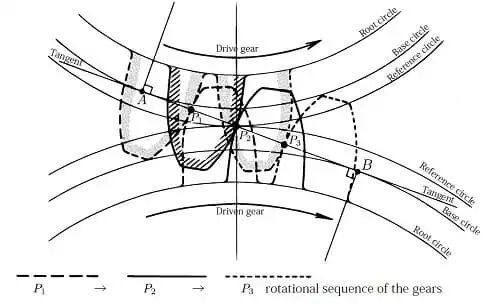
然而,传统直齿轮和斜齿轮存在本质性的运动约束。直齿轮只能实现平行轴间的运动传递,而斜齿轮虽然可以处理相交轴传动,但其运动仍局限于单一平面内的旋转。这种单自由度传动的限制源于齿轮副的刚性约束特性:两个啮合齿轮之间只能产生一个相对旋转自由度,其他五个自由度均被完全约束。
球形齿轮的结构创新
球形齿轮系统通过根本性的几何结构创新突破了传统齿轮的运动限制。其核心组成包括一个十字球体(Cross Spherical Gear)和两个鞍形齿轮(Monopole Gear)。
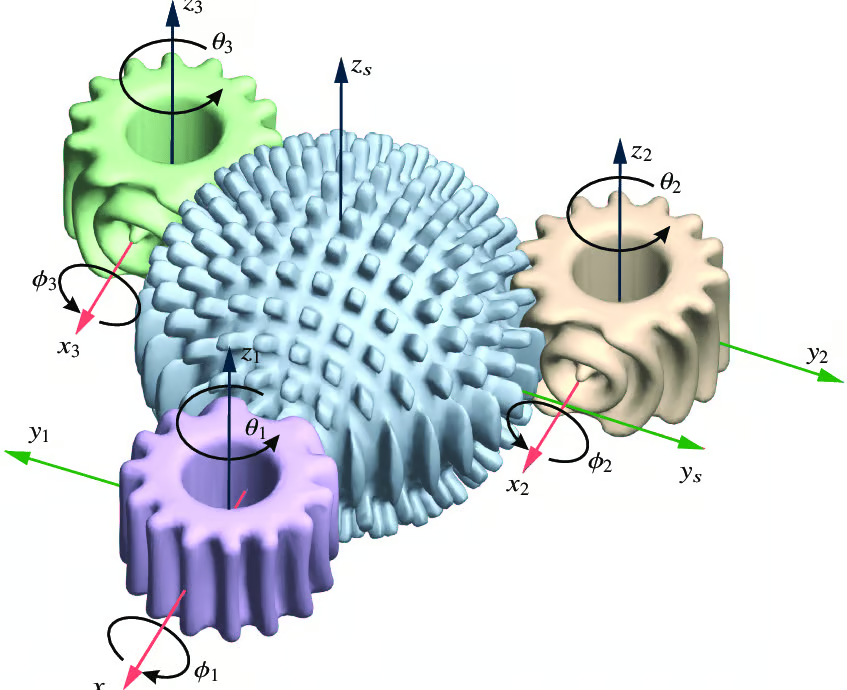
十字球体的几何构型基于球坐标系统,其表面加工有沿经线和纬线分布的齿廓。这些齿廓遵循球面渐开线原理,即传统平面渐开线在球面上的拓扑映射。球面渐开线的数学描述需要引入球面几何学,其参数方程在球坐标系(r,θ,φ)中可表示为:
θ(t) = θ₀ + ∫₀ᵗ cos(β(τ))dτ
φ(t) = φ₀ + ∫₀ᵗ sin(β(τ))dτ
其中β(t)为球面上齿廓的螺旋角函数。
鞍形齿轮的设计基于双曲面几何,其齿廓与十字球体表面形成线接触啮合。通过精确控制两个鞍形齿轮的相对位置和转速,可以实现对十字球体三个旋转自由度的独立控制。
球形齿轮的运动学特征
球形齿轮系统的运动学模型需要考虑球面约束条件下的多体动力学。设十字球体的三个欧拉角为α、β、γ,分别对应滚转、俯仰和偏航运动,则系统的运动学方程可写为:
[ω₁] [Aₓ₁ Aₓ₂] [Ω₁]
[ω₂] = [Aᵧ₁ Aᵧ₂] [Ω₂]
[ω₃] [Aᵤ₁ Aᵤ₂]
其中ω₁、ω₂、ω₃为十字球体的三轴角速度,Ω₁、Ω₂为两个鞍形齿轮的输入角速度,A为耦合系数矩阵。
与传统万向节相比,球形齿轮具有显著优势。万向节虽然能实现多自由度传动,但存在不等速传动特性和奇异点问题。球形齿轮通过齿廓啮合实现无滑动传动,传动比精确且可预测,同时具备更大的工作角度范围。
二、ABENICS技术在机器人关节中的应用
ABENICS机构概述
ABENICS(Active Ball Joint Mechanism with Three-DoF Based on Spherical Gear Meshings)技术由日本山形大学多田隈理一郎教授实验室开发。该技术的核心创新在于将球形齿轮机构应用于机器人关节设计,实现了单一机械结构内的三自由度主动控制。
ABENICS的设计理念源于对生物关节的仿生学研究。人体肩关节作为典型的球窝关节,可以实现三个旋转自由度的协调运动。传统机器人实现相同功能需要三个串联的旋转关节,导致结构复杂、惯量大、控制困难等问题。ABENICS通过单一球形齿轮机构直接实现三自由度运动,从根本上简化了机械结构。
三自由度实现原理
ABENICS机构的三自由度控制基于球形齿轮的差动传动原理。两个鞍形齿轮分别由独立的电机驱动,通过控制其转速和方向的组合,可以实现十字球体绕三个正交轴的旋转运动。
俯仰(Pitch)运动通过两个鞍形齿轮的同向等速转动实现,此时十字球体绕其水平轴旋转。偏航(Yaw)运动则通过两个鞍形齿轮的反向等速转动产生,十字球体绕垂直轴转动。滚转(Roll)运动的实现最为复杂,需要两个鞍形齿轮以特定的速度差进行转动。
运动学正解问题涉及从两个输入电机的角位置计算十字球体的三维姿态。设两个鞍形齿轮的角位置为θ₁和θ₂,则十字球体的欧拉角(α,β,γ)可通过以下变换获得:
α = k₁(θ₁ + θ₂)
β = k₂(θ₁ - θ₂)
γ = k₃f(θ₁,θ₂)
其中k₁、k₂、k₃为传动系数,f(θ₁,θ₂)为非线性耦合函数。
运动学逆解的求解相对复杂,需要根据期望的十字球体姿态反推两个电机的控制指令。由于系统存在运动学耦合,通常需要采用数值迭代方法求解。
与传统机器人关节的技术对比
ABENICS球形齿轮关节与传统串联关节在多个方面存在显著差异。结构复杂度方面,传统三自由度机器人关节需要三个独立的旋转关节串联组成,每个关节包含电机、减速器、轴承、编码器等组件。ABENICS仅需两个驱动电机和一套球形齿轮机构,结构简化程度超过60%。
体积和重量的对比同样明显。传统串联关节的总长度通常为300-500mm,重量在5-8kg范围内。ABENICS机构的轴向尺寸可压缩至150mm以内,重量减轻30%以上,这一优势在航空航天和移动机器人应用中尤为重要。
运动范围分析显示,传统串联关节虽然理论上可以实现任意角度的旋转,但受到关节间干涉的限制,实际工作空间呈现复杂的不规则形状。ABENICS的工作空间更接近球形,在±45°的锥角范围内具有良好的运动连续性。
传动精度方面,传统关节的累积误差随关节数增加而放大,典型的三关节系统末端精度约为±0.1mm。ABENICS通过齿轮直接传动避免了多级误差累积,理论精度可达±0.05mm。
能量效率的对比需要考虑多个因素。传统串联关节在运动过程中需要克服各关节的摩擦阻力,且远端关节需要驱动整个近端结构的惯量。ABENICS的集中式驱动方式避免了这一问题,在典型工况下能耗降低15-20%。
三、技术挑战与产业化障碍
3.1 制造难度分析
球形齿轮的制造精度要求极其严格。十字球体表面的球面齿廓需要达到微米级的几何精度,这对五轴数控加工设备提出了严苛要求。传统的三轴或四轴数控机床无法完成球面齿廓的连续加工,必须采用五轴联动数控系统。
五轴加工的刀具轨迹规划面临多重技术难题。首先是刀具与工件的干涉检测,球面加工过程中刀具姿态需要实时调整以避免碰撞。其次是表面质量控制,球面齿廓的表面粗糙度Ra值需要控制在0.4μm以内,这要求加工参数的精确优化。最后是加工效率问题,复杂的刀具路径导致加工周期长,单件加工时间可达15-20小时。
加工工艺参数的控制包括主轴转速、进给速度、切削深度等多个方面。球面加工时切削条件不断变化,需要采用自适应控制策略。实际生产中发现,主轴转速控制在1200-1500rpm,进给速度0.3-0.5mm/min时可获得较好的表面质量,但这一参数组合严重限制了生产效率。
材料选择和热处理技术同样关键。早期的ABENICS原型采用工程塑料制造,虽然加工相对简单,但强度和耐磨性无法满足实际应用需求。金属球形齿轮需要选择高强度合金钢,如SCM440或SNCM815,碳含量控制在0.4-0.6%之间。
热处理变形控制是另一技术难点。球形齿轮在渗碳淬火过程中容易产生不均匀变形,导致齿廓精度下降。日本的研究表明,采用真空渗碳和分级淬火工艺,配合精确的夹具系统,可将热处理变形量控制在10μm以内。
3.2 应用局限性
奇异点(Singularity)问题是ABENICS系统的固有缺陷。当系统处于特定构型时,两个鞍形齿轮的转动无法产生十字球体某个方向的旋转,导致该自由度暂时失效。数学上,这对应于运动学雅可比矩阵的奇异性:
J = ∂(α,β,γ)/∂(θ₁,θ₂)
当det(J)=0时,系统进入奇异构型。
奇异点附近的控制稳定性问题尤为突出。在奇异构型附近,微小的输入变化可能导致输出的剧烈变化,控制系统需要采用特殊的奇异性避免算法。常用的方法包括工作空间限制、运动路径规划和阻尼最小二乘法等。
负载能力限制源于球面接触的应力集中效应。根据赫兹接触理论,球面接触的最大接触应力为:
σₘₐₓ = 0.578(F·E*/R*)^(1/3)
其中F为法向载荷,E为等效弹性模量,R为等效曲率半径。
计算表明,直径100mm的球形齿轮系统最大扭矩传递能力约为50N·m,远低于同尺寸行星减速器的200-300N·m。这一限制使得ABENICS主要适用于轻载精密应用,难以满足重载工业机器人的需求。
与主流减速器的对比分析显示,谐波减速器的扭矩密度可达1.5-2.0N·m/kg,RV减速器更高达3.0N·m/kg,而ABENICS系统目前仅为0.8N·m/kg左右。这一差距限制了其在高负载应用中的推广。
3.3 成本与量产瓶颈
制造成本结构分析表明,设备投资占据了总成本的主要部分。一套完整的五轴加工中心售价在300-500万元人民币之间,而传统齿轮加工只需要普通车床和铣床。设备的高投入直接推高了产品成本。
工艺稳定性对良品率的影响不容忽视。目前球形齿轮的加工良品率约为70-80%,而传统齿轮可达95%以上。不良品的产生主要集中在球面齿廓精度超差和表面缺陷两个方面。每提高1%的良品率,单件成本可降低约3-5%。
规模化生产的成本曲线呈现典型的规模效应特征。在年产量1000件以下时,单件制造成本高达15000-20000元。当年产量达到10000件时,成本可降至8000-10000元。只有年产量超过50000件,成本才能降到与传统减速器相当的3000-5000元水平。
产业化进展方面,日本日精株式会社(NISSEI)与兼松株式会社(Kanematsu)在2025年6月签署了球形齿轮量产协议,计划于2027年实现全球首次商业化量产。该计划的技术可行性基于以下几个关键突破:金属化制造工艺的成熟、五轴加工精度的提升以及批量生产良品率的改善。
预计初期产能为年产2000-3000套,主要面向航空航天、精密仪器和特殊机器人应用。到2030年,产能目标为10万套/年,届时成本有望降至现有水平的50%以下。
商业化挑战主要来自三个方面。首先是市场接受度问题,下游客户对新技术的验证周期通常为2-3年,期间需要大量的技术支持和风险承担。其次是与成熟技术的竞争,谐波减速器和RV减速器经过数十年发展,在可靠性和成本控制方面具有显著优势。最后是供应链配套,球形齿轮需要专用的加工设备和工艺,产业链配套尚不完善。
技术发展趋势表明,球形齿轮的成本降低路径主要包括:加工工艺的优化改进、材料技术的突破创新、设计方法的迭代升级以及规模化效应的逐步显现。预计在2030年前后,球形齿轮将在特定细分领域实现商业化突破,成为机器人关节技术的重要选择之一。
随着人形机器人、协作机器人和空间机器人等新兴应用领域的快速发展,对关节系统的小型化、轻量化和多自由度集成需求日益迫切,这为球形齿轮技术提供了重要的市场机遇。技术成熟度的提升和制造成本的下降将是决定其产业化成功的关键因素。
2025年,人形机器人产业迎来爆发拐点。特斯拉Optimus量产在即,华为、宇树等企业加速技术突破,行业正从“实验室研发”向“规模化落地”跃迁为打通产业链上下游协作壁垒,艾邦机器人正式组建"人形机器人全产业链交流群",覆盖金属材料、复合材料、传感器、电机、减速器等全硬件环节,助力企业精准对接资源、共享前沿技术!
扫码关注公众号,底部菜单申请进群

